Оценка Покрытия Программы и Проекта
Тестирование программы Р по некоторому критерию С означает покрытие множества компонентов программы P М = {m1...mk} по элементам или по связям
T = {t1...tn} - кортеж неизбыточных тестов ti.
Тест ti неизбыточен, если существует покрытый им компонент mi из M(P,C), не покрытый ни одним из предыдущих тестов t1...ti-1. Каждому ti соответствует неизбыточный путь pi - последовательность вершин от входа до выхода.
V(P,C) - сложность тестирования Р по критерию С - измеряется max числом неизбыточных тестов, покрывающих все элементы множества M(P,C)
DV(P,C,Т) - остаточная сложность тестирования Р по критерию С - измеряется max числом неизбыточных тестов, покрывающих элементы множества M(P,C), оставшиеся непокрытыми, после прогона набора тестов Т. Величина DV строго и монотонно убывает от V до 0.
TV(P,C,Т) = (V-DV)/V - оценка степени тестированности Р по критерию С.
Критерий окончания тестирования TV(P,C,Т)



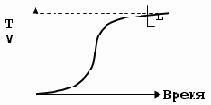
Рис. 4.1. Метрика оттестированности приложения
Рассмотрим две модели программного обеспечения, используемые при оценке оттестированности.
Для оценки степени оттестированности часто используется УГП - управляющий граф программы. УГП многокомпонентного объекта G (Рис. 4.2, Пример 4.4), содержит внутри себя два компонента G1 и G2, УГП которых раскрыты.
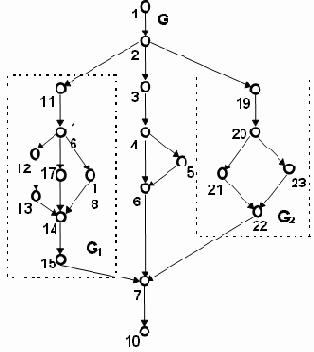
Рис. 4.2. Плоская модель УГП компонента G
В результате УГП компонента G имеет такой вид, как если бы компоненты G1 и G2 в его структуре специально не выделялись, а УГП компонентов G1 и G2 были вставлены в УГП G. Для тестирования компонента G в соответствии с критерием путей потребуется прогнать тестовый набор, покрывающий следующий набор трасс графа G (Пример 4.1):
P1(G) = 1-2-3-4-5-6-7-10; P2(G) = 1-2-3-4-6-7-10; P3(G) = 1-2-11-16-18-14-15-7-10; P4(G) = 1-2-11-16-17-14-15-7-10; P5(G) = 1-2-11-16-12-13-14-15-7-10; P6(G) = 1-2-19-20-23-22-7-10; P7(G) = 1-2-19-20-21-22-7-10; Пример 4.1. Набор трасс, необходимых для покрытия плоской модели УГП компонента G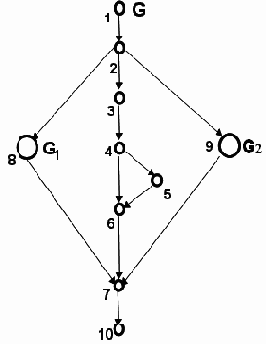
Рис. 4.3. Иерархическая модель УГП компонента G
УГП компонента G, представленный в виде иерархической модели, приведен на Рис. 4.3, Пример 4.5. В иерархическом УГП G входящие в его состав компоненты представлены ссылками на свои УГП G1 и G2 (Рис. 4.4, Пример 4.5)
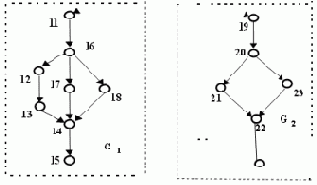
Рис. 4.4. Иерархическая модель: УГП компонент G1 и G2
Для исчерпывающего тестирования иерархической модели компонента G в соответствии с критерием путей требуется прогнать следующий набор трасс (Пример 4.2):
P1(G) = 1-2-3-4-5-6-7-10; P2(G) = 1-2-3-4-6-7-10; P3(G) = 1-2-8-7-10; P4(G) = 1-2-9-7-10. Пример 4.2. Набор трасс, необходимых для покрытия иерархической модели УГП компонента GПриведенный набор трасс достаточен при условии, что компоненты G1 и G2 в свою очередь исчерпывающе протестированы. Чтобы обеспечить выполнение этого условия в соответствии с критерием путей, надо прогнать все трассы Пример 4.3.
P11(G1)=11-16-12-13-14-15; P21(G2)=19-20-21-22; P12(G1)=11-16-17-14-15; P22(G2)=11-16-18-17-14-15 P13(G1)=19-20-23-22. Пример 4.3. Набор трасс иерархической модели УГП, необходимых для покрытия УГП компонентов G1 и G2Оценка степени тестированности плоской модели определяется долей прогнанных трасс из набора необходимых для покрытия в соответствии с критерием С.
(1) TV(G,С) = (V-DV)/V =


где PTi(G) - тестовый путь (ti) в графе G плоской модели равен 1, если он протестирован (прогнан), или 0, если нет.
Например, если в УГП (Пример 4.1) тесты t6 и t8, которым соответствуют трассы P6 и P8, не прогнаны, то в соответствии с соотношением (1) для TV(G,С) степень тестированности будет оценена в 0.71.
Оценка тестированности иерархической модели определяется на основе учета оценок тестированности компонентов. Если трасса некоторого теста tj УГП G включает узлы, представляющие компоненты Gj1,..Gjm, оценка TV степени тестированности которых известна, то оценка тестированности PTi(G) при реализации этой трассы определяется не 1, а минимальной из оценок TV для компонентов.
Интегральная оценка определяется соотношением (2):
(2) TV(G,C) = (V-DV)/V = (



где PTi(G) - тестовый путь (ti) в графе G равен 1, если протестирован, или 0, если нет. В путь PTi графа G может входить j узлов модулей Gij со своей степенью тестированности TV(Gij,С) из которых мы берем min, что дает худшую оценку степени тестированности пути.
// Пример плоской модели проекта public void G() { int TerminalStatus=0, CommandStatus=0; bool IsPresent=true, CommandFound=true; 1 Init(); 2 switch (TerminalStatus) { case 11 : 11 AddCommand(); 16 switch (CommandStatus) { case 12 : 12 GetMessage(); 13 ClearQueue(); break; case 17 : 17 ClearQueue(); break; case 18 : 18 DumpQueue(); break; } 14 ProcessCommand(); 15 Commit(); break; case 3 : 3 AskTerminal(); 4 if (IsPresent) { 5 Connect(); } 6 RebuildQueue(); break; case 19 : 19 SearchValidCommand(); 20 if (CommandFound) { 21 AnalyzeCommand(); } else { 23 LogError(); } 22 MoveNextCommand(); break; } 7 LogResults(); 10 DisposeAll(); } Пример 4.4. Пример программы для плоской модели (Рис. 4.2) // Пример плоской модели проекта void G() { int TerminalStatus=0, CommandStatus=0; int IsPresent=1, CommandFound=1; 1 Init(); 2 switch (TerminalStatus) { case 11 : 11 AddCommand(); 16 switch (CommandStatus) { case 12 : 12 GetMessage(); 13 ClearQueue(); break; case 17 : 17 ClearQueue(); break; case 18 : 18 DumpQueue(); break; } 14 ProcessCommand(); 15 Commit(); break; case 3 : 3 AskTerminal(); 4 if (IsPresent) { 5 Connect(); } 6 RebuildQueue(); break; case 19 : 19 SearchValidCommand(); 20 if (CommandFound) { 21 AnalyzeCommand(); } else { 23 LogError(); } 22 MoveNextCommand(); break; } 7 LogResults(); 10 DisposeAll(); } Пример 4.4.1. Пример программы для плоской модели (Рис. 4.2) // Пример иерархической модели проекта public void G1() { int CommandStatus=0; AddCommand(); switch (CommandStatus) { case 12 : GetMessage(); ClearQueue(); break; case 17 : ClearQueue(); break; case 18 : DumpQueue(); break; } ProcessCommand(); Commit(); } public void G2() { bool CommandFound=true; SearchValidCommand(); if (CommandFound) { AnalyzeCommand(); } else { LogError(); } MoveNextCommand(); } public void G() { int TerminalStatus=0; bool IsPresent=true; 1 Init(); 2 switch (TerminalStatus) { case 11 : 8 G1(); break; case 3 : 3 AskTerminal(); 4 if (IsPresent) { 5 Connect(); } 6 RebuildQueue(); break; case 19 : // Пример иерархической модели проекта - продолжение 9 G2(); break; } 7 LogResults(); 10 DisposeAll(); } Пример 4.5.
Пример программы для иерархической модели (Рис. 4.3) // Пример иерархической модели проекта void G1() { int CommandStatus=0; AddCommand(); switch (CommandStatus) { case 12 : GetMessage(); ClearQueue(); break; case 17 : ClearQueue(); break; case 18 : DumpQueue(); break; } ProcessCommand(); Commit(); } void G2() { intl CommandFound=1; SearchValidCommand(); if (CommandFound) { AnalyzeCommand(); } else { LogError(); } MoveNextCommand(); } void G() { int TerminalStatus=0; int IsPresent=1; 1 Init(); 2 switch (TerminalStatus) { case 11 : 8 G1(); break; case 3 : 3 AskTerminal(); 4 if (IsPresent) { 5 Connect(); } 6 RebuildQueue(); break; case 19 : 9 G2(); break; } 7 LogResults(); 10 DisposeAll(); } Пример 4.5.1. Пример программы для иерархической модели (Рис. 4.3)
